بخش اول: پردازش بلادرنگ سیگنال های دیجیتال DSP:

به منظور پیاده‌سازی هر الگوریتم پردازش سیگنال دیجیتال DSP دو راه‌کار وجود دارد. یکی پردازش غیر بلادرنگ که تمام عملیات بر روی سیگنال‌های صورت می‌گیرد که به صورت دیجیتال ذخیره شده‌اند. در این نوع، پردازش صورت گرفته تابعی از زمان حقیقی نمی‌باشد. در مقابل پردازش سیگنال های بلادرنگ (Real-time signal processing) نیاز به درنظر گرفتن ملاحظات سخت‌افزاری و نرم‌افزاری دقیقی بر اساس Timeframe‌ داده شده، دارد که در ادامه به برخی از این موارد اشاره می‌شود.

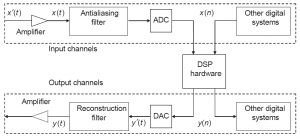
در شکل بالا یک بلوک دیاگرام ساده‌ی یک سیستم DSP نمایش داده شده است. همان‌طور که در این شکل مشاهده می‌شود یک سیگنال آنالوگ واقعی به یک سیگنال دیجیتال تبدیل شده و پس از اعمال پردازش در سخت‌افزار DSP مجدداً به سیگنال آنالوگ تبدیل می‌گردد.

• نمونه‌برداری:

همان‌طور که در شکل قبل مشاهده می‌شود سیگنال آنالوگ پس از عبور از مبدل آنالوگ به دیجیتال ADC‌ به سیگنال دیجیتال$x(n)$ تبدیل می‌گردد. تبدیل آنالوگ به دیجیتال شامل دو بخش می‌شود. دیجیتیزاسیون که شامل گسسته‌ سازی در حوزه‌ی زمان و کوانتیزاسیون که شامل گسسته‌سازی دامنه‌ي سیگنال آنالوگ می‌شود.

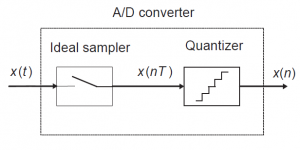یکی از ابتدایی‌ترین توابع مورد استفاده در نمونه‌برداری همان‌طور که در شکل قبل نشان‌ داده‌ شده است، نمونه‌بردار “نمونه بردار و نگه‌دار” (Sample-and-hold) می‌باشد. روال کار این تابع به این صورت است که سطح سیگنال نمونه‌برداری شده را تا ورود نمونه‌ي بعدی نگه می‌دارد. بنابراین تبدیل آنالوگ به دیجیتال صورت گرفته شامل موارد زیر است:

 برداشتن‌ نمونه‌هایی در زمان‌های هم فاصله‌ی$nT$ از سیگنال ورودی آنالوگِ $x(t)$. خروجی این مرحله سیگنال گسسته شده‌ي $x(nT)$ می‌باشد که دامنه‌ی پیوسته دارد.

 کوانتیزه شدن دامنه‌ی پیوسته‌ی هر یک از سیگنال‌های زمان گسسته‌ی $x(nT)$ در هر یک از ${{2}^{B}}$ سطح کوانتیزاسیون که در این‌جا $B$ در واقع تعداد بیت‌های مبدل است که رزولوشن مبدل نیز نامیده می‌شود.

برای بازنمایش دقیق سیگنال $x(t)$ از روی سیگنال $x(nT)$ می‌باید شرط زیر برقرار باشد:

${{f}_{s}}\ge 2{{f}_{m}}$

که در این‌جا ${{f}_{s}}=\frac{1}{T}$  فرکانس نمونه‌برداری و ${{f}_{m}}$ پهنای باند سیگنال ورودی $x(t)$ است.

نامساوی فوق به قضیه‌ی شانون موسوم است.

طبق این قضیه، چناچه فرکانس نمونه‌برداری بزرگتر یا مساوی دو برابر بالاترین مؤلفه‌ی فرکانسی موجود در سیگنال آنالوگ$x(t)$ باشد، این سیگنال به طرز مطلوبی از روی سیگنال زمان گسسته‌ی$x(nT)$ قابل بازسازی است. همچنین فرکانس ${{f}_{N}}={{f}_{s}}/2$ به فرکانس نایکوئیست و بازه‌ي فرکانسی$[-{{f}_{s}}/2, {{f}_{s}}/2]$ به بازه‌ی نایکوئیست معروف است. به بیان دیگر اگر سیگنال آنالوگی که می‌خواهیم با فرکانس نمونه‌برداری ${{f}_{s}}$ گسسته‌ سازی شود دارای مؤلفه‌های فرکانسی بزرگتر از${{f}_{s}}/2$ باشد، در حوزه‌ی فرکانس پدیده‌ی همپوشانی بین مؤلفه‌های بالاتر با مؤلفه‌های موجود در بازه‌ي نایکوئیست یا اصطلاحاً فولدینگ رخ می‌دهد.

در بسیاری از کابردهای عملی، سیگنال آنالوگ ورودی دارای مؤلفه‌های مهم فرکانسی بالاتر از فرکانس مطلوب ما برای نمونه‌برداری می‌باشد.یکی دیگر از موارد رایج وجود نویزهای با پهنای باند بالاتر از فرکانس مدنظر می‌باشد.

البته در برخی از کاربردهای مشخص، امکان تعیین نرخ نمونه‌برداری بر اساس مشخصات سیستم تحت طراحی وجود دارد.

به عنوان مثال در اکثر سیستم‌های مخابره‌ی صوت،‌ نرخ نمونه‌برداری در حدود 8 کیلوهرتز تعریف می‌شود. بنابراین به منظور ارضای قضیه‌ی شانون باید مؤلفه‌های فرکانسی‌ای که بیش از نصف 8 کیلوهرتز، یعنی بیش از 4 کیلوهرتز (فرکانس نایکوئیست) می‌باشند، باید به نحوی حدف یا به شدت تضعیف گردند.

این امر با طراحی یک فیلتر پایین‌گذر antialiasing با فرکانس قطعی معادل با

${{f}_{c}}\le \frac{{{f}_{s}}}{2}$

حاصل می‌گردد. البته در موارد عملی بهتر است به جای یک فیلتر پایین‌گذر از یک فیلتر میان‌گذر استفاده شود تا بتوان هرگونه آف‌ست DC‌ یا وزوزهای 60 هرتز یا هرگونه نویز فرکانس پایین دیگری را نیز حذف کرد. یکی از فیلترهای بسیار پر استفاده در سیستم‌های مخابراتی، فیلتر میان‌گذری است که فرکانس‌های بین 300 هرتز تا 3400 هرتز از آن عبور می‌کنند.

در ادامه در همین ارتباط چند استاندارد جهانی ذکر می‌گردد.

1- مجمع بین‌المللی مخابرت (International Telecommunication Union) موسوم به ITU استانداردی برای کدینگ/دیکیدنگ گفتار به شماره‌ی ITU-T G.729 و ITU-T C.723.1 ارائه داده است. در این استاندارد نرخ نمونه‌برداری\[{{f}_{s}}=8 KHz\] تعریف شده است. که از این‌جا پریود نمونه‌برداری 125 میکروثانیه درمی‌آید.

2- در استانداردهای مربوط به کدینگ مخابرات پهن‌باند، مثلاً استاندارهای ITU-T G.722 یا ITU-T G.722.2 نرخ نمونه‌بردای ${{f}_{s}}=16KHz$  و معادلاً پریود نمونه‌بردای 62.5 میکروثانیه تعریف شده است.

3- در استانداردهای فشرده‌سازی با کیفیت صوت مانند MPEG-2 یا AAC‌ یا MP3 باند صوت از نرخ نمونه‌برداری${{f}_{s}}=48KHz$ پشتیبانی می‌کند.

در بخش‌ بعدی با مفاهیم “کوانتیزاسیون” و “دیکدینگ”   آشنا خواهیم شد.